Mamba !

丝毫没有为 RNN 和 Transformer 的离去而遗憾，立刻赶到现场的是我们的 Kobe Bryant Mamba 模型（逃）。原论文为 2024 年的 COLM 的 Outstanding paper，但先前曾被多个顶会拒绝（悲），果然搞学术投论文就像买彩票。原来这篇文章的标题为 Mamba Out，后来发现确有其文……便老实改回来了。

花と水飴、最終電車 — n-buna

Mamba 的原论文一共有惊人的 36 页，在了解 Mamba 模型之前，我们需要了解一部分前置知识，将 Mamba 模型的来龙去脉讲明白才能真正理解它到底做了什么工作。

Transformer 的问题

在我的上一篇文章中，对从 RNN 到 Transformer 模型发展的来龙去脉和相关原理进行了讲解，其中有提到 Transformer 的问题为推理阶段的计算量冗余，且参数量很大，占用显存较多。但是在训练阶段 Transformer 的注意力机制是支持高度并行计算的，其能够充分发挥 GPU 的优势。而 RNN 等模型则与 Transformer 相反，其推理过程很快，是线性复杂度，但是训练过程不支持并行。

图 1 RNN vs Transformer

所以我们自然地能够想到：有没有一种模型可以结合上面两种模型的优点，训练时支持并行，推理时又近似线性复杂度？

有的兄弟，有的，就是 Mamba 模型

状态空间模型（SSM）

上一篇文章我们有讲到 RNN 的状态变换和输出公式和状态空间模型有关，下面我们就详细讲解什么是状态空间模型，它和 Mamba 有什么关联。填坑最快的一集（不是）

什么是 SSM

状态空间模型（State Space Model——SSM）是一种强大的时序建模方法，它起源于控制理论和信号处理，被广泛应用于机器学习、深度学习中的序列建模场景（如语音、文本、时间序列、RL）。

用一句话来概括的话，SSM 是通过隐藏状态 \(h(t)\) 的动态演化来描述输入序列 \(u(t)\) 到输出 \(y(t)\) 的映射的模型。

连续时间 SSM 的标准形式如下：

\[\begin{align} \dot{h}(t) &= A h(t) + B u(t) \text{（状态更新）} \\ y(t) &= C h(t) + D u(t) \text{（输出读取）} \end{align}\]

• \(h(t) \in \mathbb{R}^N\)：隐藏状态
• \(u(t) \in \mathbb{R}^D\)：输入（例如 token embedding）
• \(y(t) \in \mathbb{R}^D\)：输出（例如下一个 token embedding）
• \(A, B, C, D\)：是参数矩阵

系统的结构图如下：

图 2 连续时间 SSM 结构图

从图中我们可以看到，这里从 x 经过 D 变换成为输出的一部分实际上是一个跳跃连接（skip connection），我们可以把它从 SSM 模型中抽取出来，于是我们可以得到如下的形式：

图 3 连续时间 SSM 结构图（跳跃连接）

然而计算机是无法处理连续信号的，所以我们需要对输入进行离散化操作，最简单的离散化操作就是每隔一段时间在原信号上进行采样，而从离散信号到连续信号则只需要将某个离散点保持（Hold）一段时间即可。

图 4 连续信号使用 Hold 方法离散化

Zero-order hold（ZOH）离散化

Zero-order hold（ZOH） 是一种假设离散时间输入在采样周期内保持不变的离散-连续变换方法。是在连续系统离散化时非常常见的一种方法。

考虑连续时间状态空间模型：

\[\begin{align} \dot{h}(t) &= A h(t) + B u(t) \\ y(t) &= C h(t) \end{align}\]

要将其离散化为步长 \(\Delta\) 的系统（即在 \(t = 0, \Delta, 2\Delta, \dots\) 上建模），使用 ZOH 后，得到如下离散模型：

\[\begin{align} h_{k+1} &= \bar{A} h_k + \bar{B} u_k \\ y_k &= C h_k \end{align}\]

其中：

\[\begin{align*} \bar{A} &= \exp(A\Delta) \\ \bar{B} &= \int_0^\Delta \exp(A\tau) \, d\tau \cdot B \\ &= A^{-1}(\bar{A} - I)B \quad \text{(若 \( A \) 可逆)} \end{align*}\]

这就是 Zero-Order Hold 离散化公式。

实际上这是常微分方程的解，详见知乎

总结：

• ZOH 假设输入信号在每个采样周期内保持恒定。
• 它使得连续时间 SSM 可以被正确、稳定地离散化为递推形式（scan-able）。
• 在现代神经 SSM（如 S4、Mamba）中用于将连续状态更新转换为高效离散扫描。

递归和卷积求解离散 SSM

经过离散化后，我们得到了下面的方程，我们想要利用神经网络求解整个过程。有两种方法供选择：递归和卷积。

\[\begin{align*} h_{t+1} &= \bar{A} h_t + \bar{B} u_t \\ y_t &= C h_t \end{align*}\]

• 递归（Recurrent）

这种方法其实就是 RNN 求解的方式，按照时间的顺序线性求解每一个时间步的结果。流程如下图所示：

图 5 递归方法求解离散 SSM

• 卷积（Convolution）

要想利用卷积的方式求解，需要先把离散 SSM 的每个解展开，如下：

\[\begin{align*} y_1 &= C \bar Bu_1 \\ y_2 &= C(\bar A \bar B u_0 + \bar B u_1) \\ y_3 &= C(\bar A^2 \bar B u_0 + \bar A \bar B u_1 + \bar B u_2) \end{align*}\]

从前三个解的格式中可以发现求解的过程可以视作如下的卷积操作：

图 6 卷积方法求解离散 SSM

这是一个一维的卷积，卷积核的维度和输入的长度相同，输入序列需要进行 padding 操作，在计算的过程中，卷积核从左向右进行移动。

使用卷积操作来求解的好处在于其可以通过并行操作进行训练加速（正如卷积神经网络那样），但是受限于其固定的核大小，它的推理并不能像 RNN 一样迅速且无限制。

有了上面的两种不同的方式，我们可以在训练阶段使用卷积，在推理时使用递归，根据不同的任务选择最高效的方法。这其实就是线性状态空间层（LSSL）做的事情。

NIPS 2021 Combining Recurrent, Convolutional, and Continuous-time Models with Linear State Space Layers

HiPPO 方法创建状态转移矩阵

矩阵 A 在整个 SSM 模型中是非常重要的，它决定了当前状态能够关注到多久之前的信息。我们需要一种能够让模型尽可能保留更长时间的信息的状态转移矩阵 A，HiPPO（High-order Polynomial Projection Operators）是其中一种解决方案。

HiPPO 是一种创新的方法，用来构建连续时间的状态空间模型（SSM），使其能够高效且稳定地记忆历史输入信息，其是 S4、S6、Mamba 等现代长序列建模模型的核心理论基础之一，通过构造出一组特殊的状态更新矩阵 \(A\) 和输入矩阵 \(B\)，使得状态 \(h(t)\) 在不断接收输入 \(u(t)\) 的过程中，始终逼近某个函数（如 \(u(\tau)\) 在过去的时间区间上的某种投影）。

• HiPPO 的目标

构建一组 ODE，使得隐藏状态 $h(t)$ 始终逼近如下投影：

\[h_n(t) \approx \langle f_t, p_n \rangle = \int_0^\infty f_t(x) p_n(x) dx\]

其中：

• \(\{p_n(x)\}_{n=0}^{N-1}\) 是一组正交多项式基（如 Legendre、Laguerre）

• \(h_n(t)\) 是第 \(n\) 个投影系数

• 核心数学形式：HiPPO ODE

HiPPO 论文证明，这样的投影系数可以由以下微分方程组逼近：

\[\dot{h}(t) = A h(t) + B u(t)\]

• \(A \in \mathbb{R}^{N \times N}\)、\(B \in \mathbb{R}^{N}\)

• \(A, B\) 是专门设计的：它们与所选的正交多项式族有关

• HiPPO-LegS（基于 Legendre 多项式）

\[A_{ij} = (2i+1)\left[ \delta_{ij} - 1_{\{i<j\}} \right],\quad B_i = (2i + 1)\]

这些矩阵有高度结构化的形式：

• \(A\)：上三角、低秩

• 可高效计算 \(\exp(A\Delta)\) 和 \(\int_0^\Delta \exp(A\tau) d\tau B\)

• HiPPO-LegT

HiPPO-LegT（Legendre Time-weighted）变体，也叫 HiPPO-LegT matrix。它是 HiPPO 框架下的一种构造方法，用于以递减权重对过去输入进行投影，强调最近输入的重要性，并以时间加权的方式衰减较旧的信息。

HiPPO matrix \(A\) 的定义如下：

\[A_{nk} = \begin{cases} \sqrt{(2n + 1)} \cdot \sqrt{(2k + 1)}, & k \leq n \\ 0, & k > n \end{cases}\]

并且主对角线处 \(A_{nn} = n + 1\)，这是为了保证矩阵具有良好的数值稳定性和谱性质。

• 对比：HiPPO-LegT vs HiPPO-LegS

特征	HiPPO-LegS	HiPPO-LegT ✅（图中形式）
基函数	Shifted Legendre	Time-weighted Legendre
应用目标	记忆整个输入区间	强化最近信息，衰减旧信息
矩阵结构	上三角（structured）	下三角（如图）
$A_{nk}$ 构造方式	复杂的上三角组合	$A_{nk} = \sqrt{(2n+1)(2k+1)}$ for $k \leq n$
是否对角主导	是	是（主对角线 = $n+1$）
实际表现	稳定记忆长序列	更适合关注最近的局部上下文

HiPPO-LegT 更强调近期输入，抑制旧的信息，适合 scan、RNN、state space 等结构作为连续更新项，被用在一些 Mamba-like 模型中，用于高效建模长序列依赖。这里我们所使用的就是 HiPPO-LegT

将 HiPPO 应用于前面提到的递归或卷积表示的方法来处理长序列依赖问题，这样得到的模型就是 Structured State Space for Sequences（S4）模型了，其是一种能够高效处理长序列的模型，包含下面三种要素：

1. 状态空间模型
2. 使用 HiPPO 解决长序列依赖
3. 使用离散化手段来创建递归或卷积表示

图 7 Structured State Space for Sequences 构成图

这里有一篇介绍 S4 模型的文章，感兴趣的可以点击查看，是 Srush 大佬的文章。

S6 模型

介绍完上面的前置知识后，我们终于能够直面 Mamba 模型的重要元件 —— S6 了！

Mamba 模型最突出的两大贡献就是：

1. 提出了一种选择扫描算法，让模型能够对（不）相关的信息进行过滤
2. 提出了一种硬件感知算法，能够高效存储并行扫描算法、核融合（Kernal Fusion）、重计算（Recomputation）过程中产生的中间结果

上面这两点共同造就了 Selective State Spaces Model 或 S6 模型，它们类似自注意力之于 Transformer，构成了整个 Mamba 最为关键的部分。

线性时不变模型的缺陷

SSM 模型，包括前面我们提到的 S4 模型都是线性时不变模型（Linear Time Invariant），这是信号与系统中的概念，表示系统的参数不随时间的变化而改变。在此处体现在 SSM 的参数 A,B,C 是固定不变的。这会导致一个后果，即模型只是对整个序列有所记忆，但不会按照需求关注需要的信息。而这一点是非常重要的，Transformer 之所以能取得如此巨大的成功就在于其注意力机制可以对序列进行重要性编码。

反之，如果不能动态调整序列的权重，模型将无法具备推理能力。

另一个线性时不变系统无法实现的功能就是 Induction Heads（归纳头，是注意力头的一种，常见于上下文学习中），模型无法根据要求复现用户输入样例的格式。例如：

图 8 one-shot prompting 的一个例子

如果模型不能调整输入的权重（没有注意力）的话，它就不知道用户的需求应该对应哪部分记忆，无法做到内容感知（content-aware），从而无法根据用户需求输出和样例一致的结果。

选择扫描算法

RNN 对状态进行极致的压缩，导致其无法根据输入调整权重，而 Transformer 则相反，使用大量的资源来计算状态。S6 则是在两者之间均衡，具有两者的优点，如图 9 所示。

图 9 三个模型的 State Size 对比

S6 和 S4 在参数维度上做的改变可以从下面的图中看出：

图 10 S4 和 S6 参数维度对比

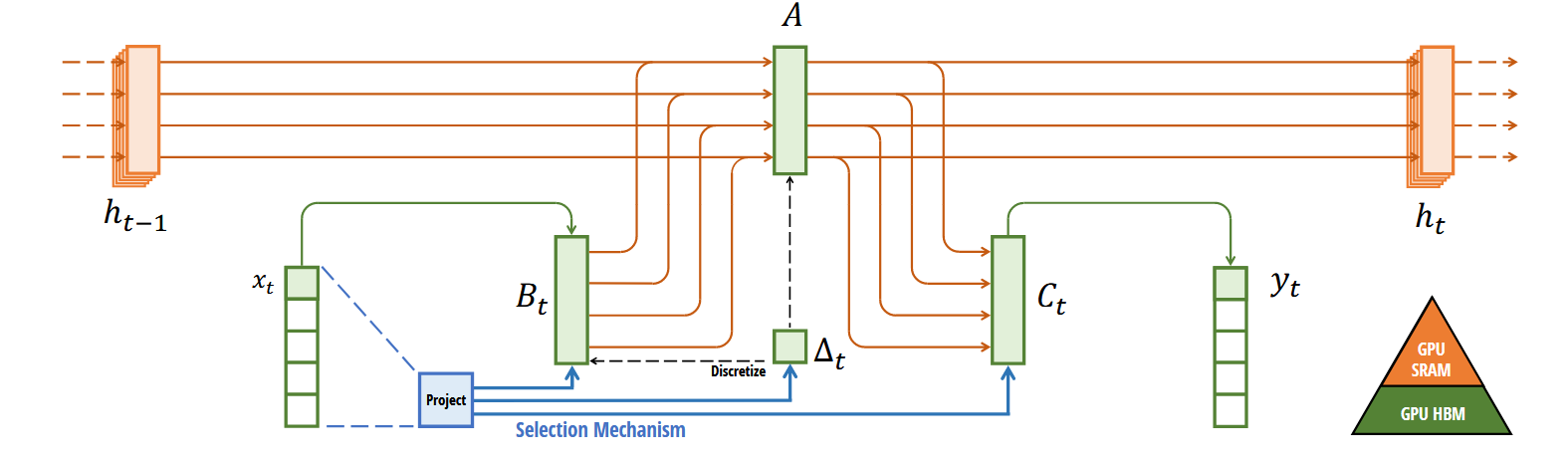
对于 S6 模型，其输入为 (batch_size, len_seq, dimention_input) = (B, L, D)，步长 \(\Delta\) 和输入为同样的尺寸，矩阵 B 和 C 的维度为 (batch_size, len_seq, dimention_hiddens) = (B, L, N)，而矩阵 A 的维度则保持不变，因为我们希望让固定输入对应的初始状态也是固定的，但状态的变换和输出会改变。

S4 和 S6 模型的伪代码如下图所示：

图 11 S4 和 S6 伪代码

图中的 \(s_B(\cdot),s_C(\cdot)\) 是线性层，输入维度是 D，输出维度为 N，\(s_\Delta\) 也是线性层，但其输入和输出维度都是 D， \(\tau_\Delta\) 是 Softplus，其是一种常用的平滑激活函数，定义如下：

\[\text{softplus}(x) = \log(1 + e^x)\]

它是 ReLU（Rectified Linear Unit）函数的平滑版本：

• ReLU:                                                     

  \[\text{ReLU}(x) = \max(0, x)\]

• Softplus:

  \[\text{softplus}(x) \approx \begin{cases} 0, & \text{if } x \ll 0 \\ x, & \text{if } x \gg 0 \end{cases}\]

• 扫描操作

由于我们的参数矩阵是随着输入而变化的，所以不能直接使用卷积操作以通过并行的方式加速训练，只能采用递归计算的方式进行。但是我们仍然可以使用并行扫描算法来对训练进行并行加速。

S6 模型中的状态转移方程可以表示为下面的形式：

\[h_t=\bar A_t h_{t-1} + \bar B_t x_t \tag{7}\]

对于这种形式，我们可以利用前缀和的方式来并行计算，其具体的方式如下图所示：

图 12 前缀和并行计算示意图

这种前缀和的方式在长序列的加法中（例如求解 \(x_1+x_2+x_3+...+x_t\)）是适用的，简单来说就类似于分治算法，将子序列分成两部分，交给两个进程并行计算。

能够这样做的前提是运算过程符合结合律，所以我们需要证明式 (7) 的求解是符合结合律的。我们可以把式 (7) 视作一个仿射变换：

\[f_t(h) = A_th+b_t\]

我们需要计算的最终结果是多个仿射变换的组合，即

\[h_t=f_{1:t}(h_0)\]

其中，\(f_{1:t} = f_t \circ f_{t-1} \circ f_{t-2} \circ \cdots \circ f_1\)

所以，我们的目标是并行计算所有的仿射组合 \(f_{1:t}\)

将仿射变换 $f(h) = A h + b$ 表示为一个扩展矩阵：

\[F = \begin{bmatrix} A & b \\ 0 & 1 \end{bmatrix}\]

这样，两个仿射变换 \(F_i, F_j\) 的组合就是矩阵乘法：

\[F_j \circ F_i \Rightarrow F_j F_i\]

于是整个问题就转化为对这些扩展矩阵 \(F_t\) 做前缀乘法：

\[F^{[1:t]} = F_t F_{t-1} \cdots F_1\]

这正好是一个典型的矩阵乘法 scan问题——是结合律成立的并行可扫描操作！所以我们就可以像图 12 显示的那样去并行计算啦！

原作者分别使用 Pytorch 框架和 Triton 语言实现了这样的算法，其效果如下图所示：

图 13 训练时间和吞吐量的对比图

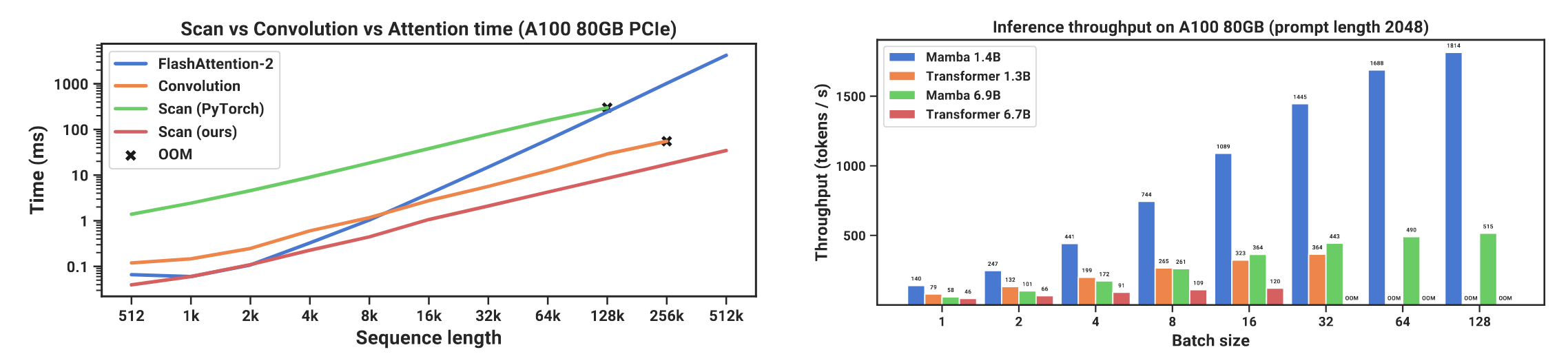
可以看到 Pytorch 对此算法的支持并不是很好，训练耗时比 FlashAttention 要久，但是如果使用 Triton 构建自定义 GPU 加速算子，就能取得比 FlashAttention 更快的训练速度。另外吞吐量方面，Mamba 相比 Transformer 可谓是遥遥领先！

重点需要关注 \(\bar A, \bar B\) 两个矩阵的爱因斯坦求和约定运算，前者是按照 ZOH 方法离散化的，但是后者则使用简单的欧拉离散化，原因是 A 更加重要，B 的离散化方法对结果的影响不大。简单介绍一下欧拉离散化方法：

假设有一个连续时间的一阶微分方程：

\[\frac{dy(t)}{dt} = f(y(t),t), y(0) = y_0\]

我们简单地将导数近似为差分：

\[\frac{dy(t)}{dt} \approx \frac{y_{k+1}-y_k}{\Delta t}\]

因此我们可以解出下一个状态的表示：

\[y_{k+1} = y_k + \Delta t \cdot f(y_k,t_k)\]

硬件感知算法

使用 GPUs 进行计算的一大缺陷就在于其 SRAM 和 DRAM 之间的 IO 太耗费时间了，特别是对于有一大堆临时变量需要来回传输的情况下，如下图所示：

图 14 SRAM 和 DRAM 之间频繁通信

Mamba 像 Flash Attention（坏，我还不知道什么是 Flash Attention，等有时间填坑吧）一样，努力减少 CPU/GPU 中 DRAM（主存）和 SRAM（片上缓存）之间的数据传输次数。它通过使用 kernel fusion（内核融合）技术，避免写入中间结果，从而连续进行计算直到完成整个操作。

DRAM（动态随机存取存储器）：通常指计算机或 GPU 的主内存，容量大但访问速度慢。 SRAM（静态随机存取存储器）：通常指 GPU 的片上缓存（如 register、shared memory、L1/L2 cache），速度快但容量小。

Kernel Fusion（内核融合） 是一种将多个 GPU 操作（kernels）合并为一个操作的技术。

在普通的模型计算中，例如：

x = torch.relu(x)
x = torch.square(x)
x = torch.sum(x)

系统会分别启动三个 GPU kernel 执行：1. ReLU kernel；2. Square kernel；3. Sum kernel，每次 kernel 调用都需要将结果写回 DRAM，再读取到 SRAM，带来频繁的数据传输开销。

Kernel Fusion 的做法是将这些操作融合为一个 kernel，一次性读取数据、连续计算、一次性写回结果。减少了多次 kernel 启动和 DRAM/SRAM 之间的数据交换。

也就是说：内核融合 = 一次性把连续的操作“打包”进一个 kernel 中，让它们在 GPU 的缓存/寄存器里完成，避免中间结果回写内存。

图 15 kernel fusion 操作

S6 模型中，将下列操作融合进一个 kernel 中：

1. 使用步长 \(\Delta\) 进行离散化
2. 选择扫描算法
3. 与输出矩阵 C 的乘法

反向传播时需要用到中间的临时状态，但我们并没有将它们存储起来，而是在反向传播的时候重新进行计算。这样做虽然表面上加大了计算量，但其实上在 SRAM 中直接计算状态比从 DRAM 中读取所有状态要来的更快。

现在我们已经介绍完 S6 模型的所有组件了，于是我们可以从图 16 中看到整个 S6 模块的构成。

图 16 整个 S6 模块的构成

Mamba

Mamba 模型是由多个 Mamba Block 组成的，Mamba Block 的构成见下图：

图 17 Mamba Block 的构成（端到端）

和 Transformer 中的解码器一样，数层的 Mamba Block 首尾连接构成了 Mamba 模型，S6 模型有如下的性质：

1. 通过离散化构成递归 SSM
2. 使用 HiPPO 初始化矩阵 A 以捕捉长期依赖
3. 使用选择扫描算法压缩信息
4. 使用硬件感知算法加速计算

下图描述了 Mamba 模型结合了 RNN 和 Transformer 模型的优点：

图 18 Mamba Block 的构成（端到端）

下图展示了 Mamba 的 Scaling Laws：

图 19 Mamba 的 scaling laws（对比其他模型）

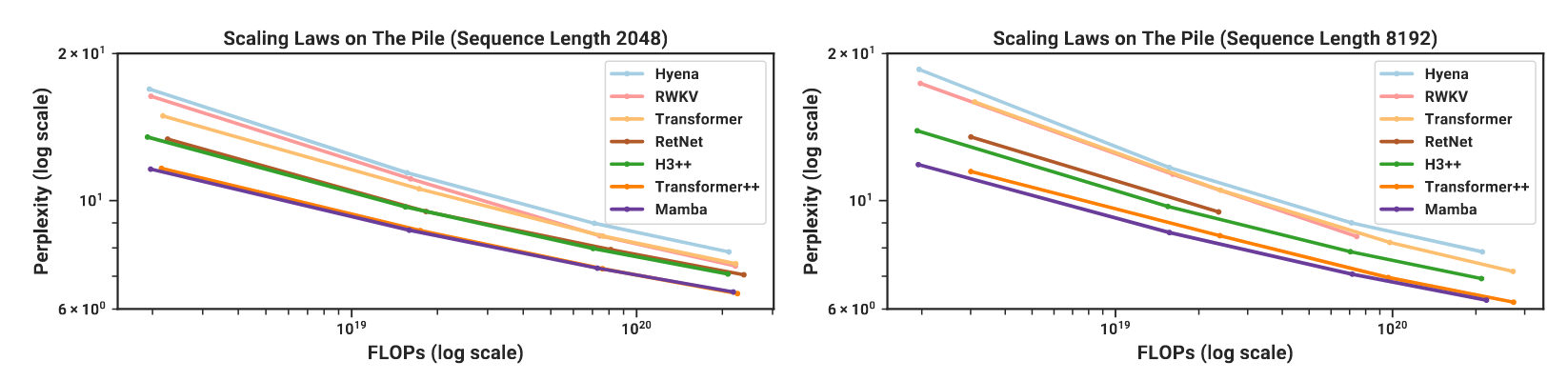
可以看见 Mamba 仍然具有和 transformer 一样的 scaling law，并且其表现和最先进的 transformer++ 相差无几，可以预见 Mamba 具有光明的未来！

代码部分我会单独写一篇博客详细讲讲。

总结

Mamba 模型堂堂讲完（其实还有很多细节，但我懒得管了），如果要总结 Mamba 模型为什么行，为什么好，归根结底是因为以下几点：

1. 身为时变模型，Mamba 能够有选择地处理状态信息，实现类似注意力机制的效果，其具有较强的编码能力
2. 推理时是 O(n) 的时间复杂度，比 Transformer 快得多
3. 能够使用扫描算法并行训练
4. 使用硬件感知算法加速计算

不过我个人认为其最重要的一点就是显著降低了推理的时间，这也是我们之前提到的 Transformer 的最大缺陷。

但是说 Mamba 想取代 Transformer 成为更强的架构，我持保留态度，Mamba 目前在我看来只是拿来处理序列模型会更高效一点。而且我目前没有看见可视化状态的工作，相比于注意力这种能够很好地可视化的机制来说可解释性不强，并且对于非序列模型的处理估计是比不过 Transformer，注意力机制本身就是无序的，是位置编码赋予了其处理有序模型的能力。反观 Mamba 模型，其整个原理都建立在时序模型上，这难免使得模型本身的 flexibility 下降。

参考资料

感谢大佬的讲解，省去了我阅读 36 页论文的时间：

A Visual Guide to Mamba and State Space Models

Mamba: The Easy Way

【论文阅读笔记】Mamba模型代码理解

The Annotated S4

如何理解 Mamba 模型 Selective State Spaces

Mamba架构中的zero order hold(zig)有什么作用

Mamba: The Hard Way

一文通透想颠覆Transformer的Mamba：从SSM、HiPPO、S4到Mamba(被誉为Mamba最佳解读)

原论文：Mamba: Linear-Time Sequence Modeling with Selective State Spaces

特别感谢：ChatGPT