大语言模型压缩方法
暑假正式开始了,论文的阅读计划也要提上日程。话说暑假真是忙碌,又要家教,又要练琴,又要科研的()
昨晚忽然得知 nbuna 结婚了,有股恍如隔世之感。


前言
5 月初阅读的一篇综述是 2022 年的,彼时大语言模型(LLM)刚开始发展,关于 LLM 的量化方法还不是很多,5202 年的现在,针对 LLM 的量化已经一批接着一批涌现出来了。为了与时俱进,我找了一篇 2024 年的综述,针对其中涉及到的量化方法进行简单的介绍。下图是论文中总结的关于 LLM 的量化方法大全,便于大家检索。

一、量化
不同量化方法的表现可以从下表中见到:
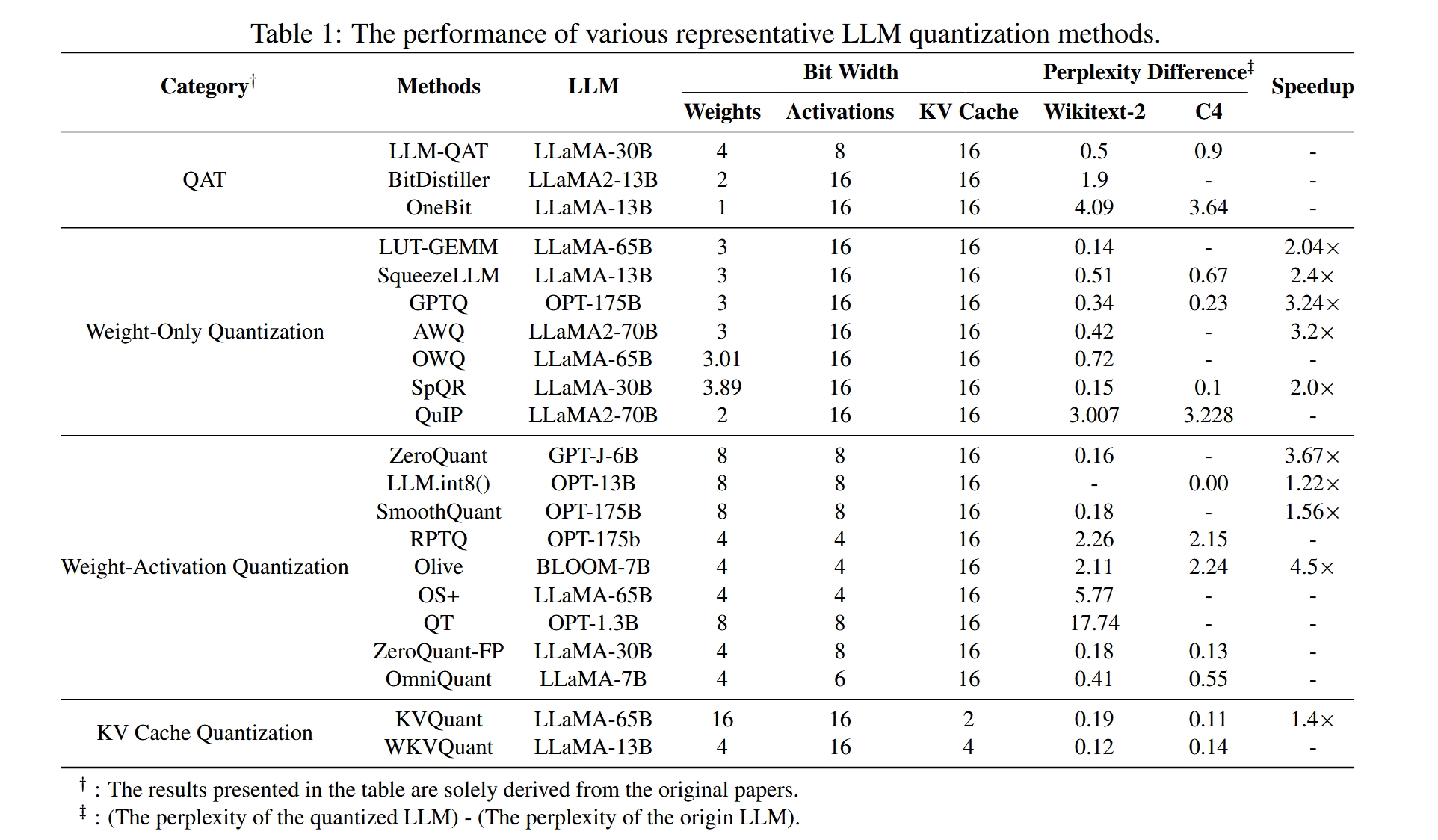
(一)量化感知训练(QAT)
(二)训练后量化(PTQ)
1. 仅量化权重
(1) LUT-GEMM
论文链接:https://arxiv.org/abs/2206.09557,引用次数:162,发表于:ICLR 2024
是一种W4/A16的量化方法,突出贡献在于其在推理过程中不需要反量化。图 1 是其简略的框架图。
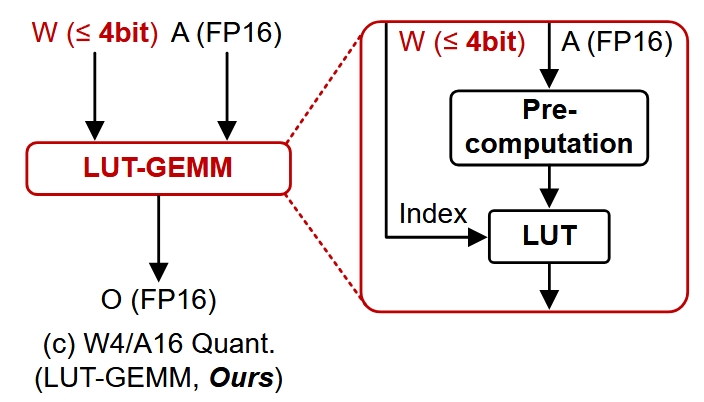
在介绍其原理之前,首先我们需要知道 LUT-GEMM 是基于 BCQ(Binary Coding Quantization)实现的,其是一种二值量化的方法,将权重向量表示成若干个经过缩放的二值向量的和:
\[\omega = \sum_{i=1}^{q} \alpha_i \boldsymbol{b_i}, \quad \alpha_i \in \mathbb{R}^+, \quad \boldsymbol{b_i} \in \{-1,+1\}^n\]简单来说,LUT 就是一张查询表(Look-up Table),根据输入的激活值进行计算,后续量化权重和输入的运算是通过查表的方式进行的。建表的原理我们通过下面的一个例子来说明。
我们假设有一个维度为 4 × 6 的 二值矩阵 \(B\),输入 \(b\) 是 6 × 1 的浮点数FP16,如下所示:
\[B = \begin{bmatrix} +1 & +1 & -1 & -1 & -1 & +1 \\ +1 & +1 & -1 & +1 & +1 & -1 \\ +1 & +1 & -1 & -1 & -1 & -1 \\ -1 & -1 & +1 & -1 & -1 & +1 \end{bmatrix}, \quad x = \begin{bmatrix} x_1 & x_2 & x_3 & x_4 & x_5 & x_6 \end{bmatrix}.\]如果我们直接计算 \(B\) 和 \(x\) 的乘积,会发现存在大量的冗余计算,例如 \(x_1+x_2-x_3\) 被重复计算了多次,这样的计算冗余会随着矩阵 B 维度的增加而增加,因此我们可以通过建表的方式来减少运算量。
具体来说,我们可以对 \(x\) 的分量进行分组,假设 \(\mu\) 个分量为一组,那么这几个分量之间的所有可能结果一共有 \(2^\mu\) 种,我们将其提前计算,并以表格的形式存储起来,等到要用的时候再进行查询即可。这一过程的时间复杂度约为 \(\mathcal{O}\big(m \cdot \frac{n}{\mu} \cdot q \big)\)
为了能够进一步加速,作者在 GPU 上实现时还将其以线程为粒度进行了优化,如下图 2 所示。
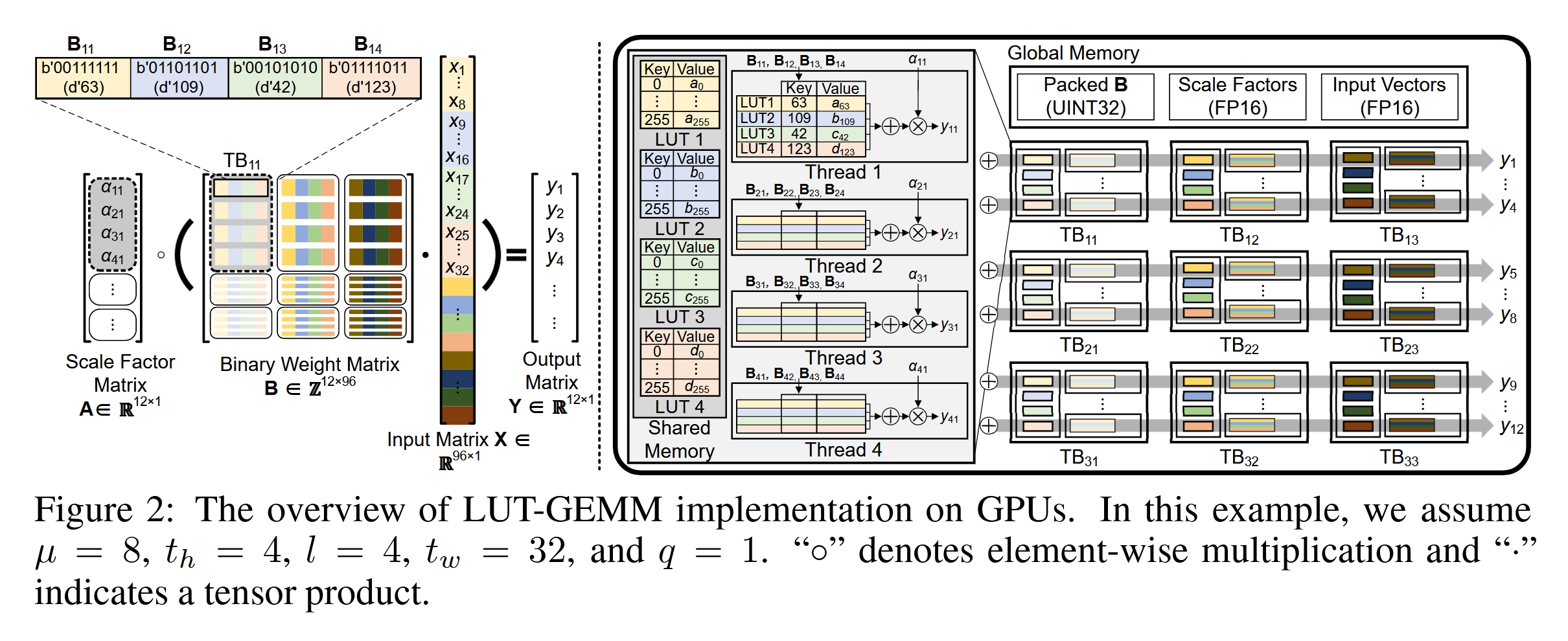
这里我们把矩阵 \(B\) 分成了九块,交给九个线程块(Thread Block)分别处理,假设一个线程块包含四个线程,一个 TB 中的四个线程共享四张 LUT,这里我们的 \(\mu=8\),即一张 LUT 由 256 项构成。这张图还是挺清晰的,整体的思想倒是并不难理解。
除此之外,为了确保量化精度,作者采用了分组量化的方法,将输入的维度进行分组,每一组共用一个缩放系数。实验证明一组的数量越多,延迟越小(矩阵乘法完成时间越短),这是由于单批量操作 (single-batch operations) 主要受限于内存 (memory-bound),并且延迟与内存占用成正比。
作者还在原本的 BCQ 的基础上加上了一个偏置项:
\[\omega = \sum_{i=1}^{q} \alpha_i \boldsymbol{b_i} + z\]这使得 BCQ 可以表示零点,成为一种非对称量化方法,同时作者还从理论上证明了经过合理的取值,BCQ 可以成为均匀量化方法。(这也是这篇文章的一个重要贡献)
(2) GPTQ
论文链接:https://arxiv.org/abs/2210.17323,引用次数:1162,发表于:ICLR 2023
是一种针对大模型的量化方法,其特点就是:适用于大模型、需要的算力少、量化模型精度损失小。最突出的贡献就是 GPTQ 是第一个能够将大模型量化到 3-4bit 的方法,其证明了对 LLM 进行量化的可行性。
GPTQ 的思想来源于 Yann LeCun 在 1990 年提出的 OBD 算法。OBD、OBS、OBC、OBQ 是一系列剪枝和量化算法,我们一一对其进行介绍。
- OBD 和 OBS
OBD 是一种剪枝算法,其思想很简单,就是希望剪枝的结果对目标函数造成的影响最小。我们对目标函数进行泰勒展开可以得到:
\[\Delta E = \sum_i g_i \Delta w_i + \frac{1}{2} \sum_i h_{ii} (\Delta w_i)^2 + \frac{1}{2} \sum_{i \neq j} h_{ij} \Delta w_i \Delta w_j + O(\Delta w^3)\]其中 g 是偏导,h 是海森矩阵,OBD 假设模型经过训练之后,其关于各维度的一阶偏导应该是 0,所以第一项直接省略,如果我们再对高阶项进行省略就得到下面的式子:
\[\Delta E = \frac{1}{2} \sum_i h_{ii} (\Delta w_i)^2 + \frac{1}{2} \sum_{i \neq j} h_{ij} \Delta w_i \Delta w_j\]OBD 算法直接忽略了交叉项,其假设每个参数对目标函数的影响是独立的。所以又把上面的第二项忽略了。
而 OBS 则没有忽略交叉项,其将剪枝问题建模成一个约束优化问题,如下:
\[\min_{\Delta \mathbf{w}, q} \frac{1}{2} \Delta \mathbf{w}^\text{T} \mathbf{H} \Delta \mathbf{w} \quad s.t. \quad \mathbf{e}_q^\text{T} \cdot \Delta \mathbf{w} + w_q = 0\]使用拉格朗日法求解得到结果:
\[\Delta \mathbf{w} = -\frac{w_q}{[\mathbf{H}^{-1}]_{qq}} \mathbf{H}^{-1} \cdot \mathbf{e}_q \quad \text{and} \quad L = \frac{1}{2} \frac{w_q^2}{[\mathbf{H}^{-1}]_{qq}}\]在剪枝的时候,每次寻找对最终目标函数影响最小的权重,设为 0,并更新其他权重,如此迭代即可。
- OBC 和 OBQ
上面的算法的问题是计算量比较大,我们需要求解海森矩阵,当模型的参数量和输入维度很大的时候,求解海森矩阵花费的时间太长。所以 OBC 采取的措施是假设参数矩阵的同一行参数互相之间是相关的,而不同行之间的参数互不相关,这样,海森矩阵就只需要在每一行内单独计算就行啦。
其实现原理的示意图如下所示:
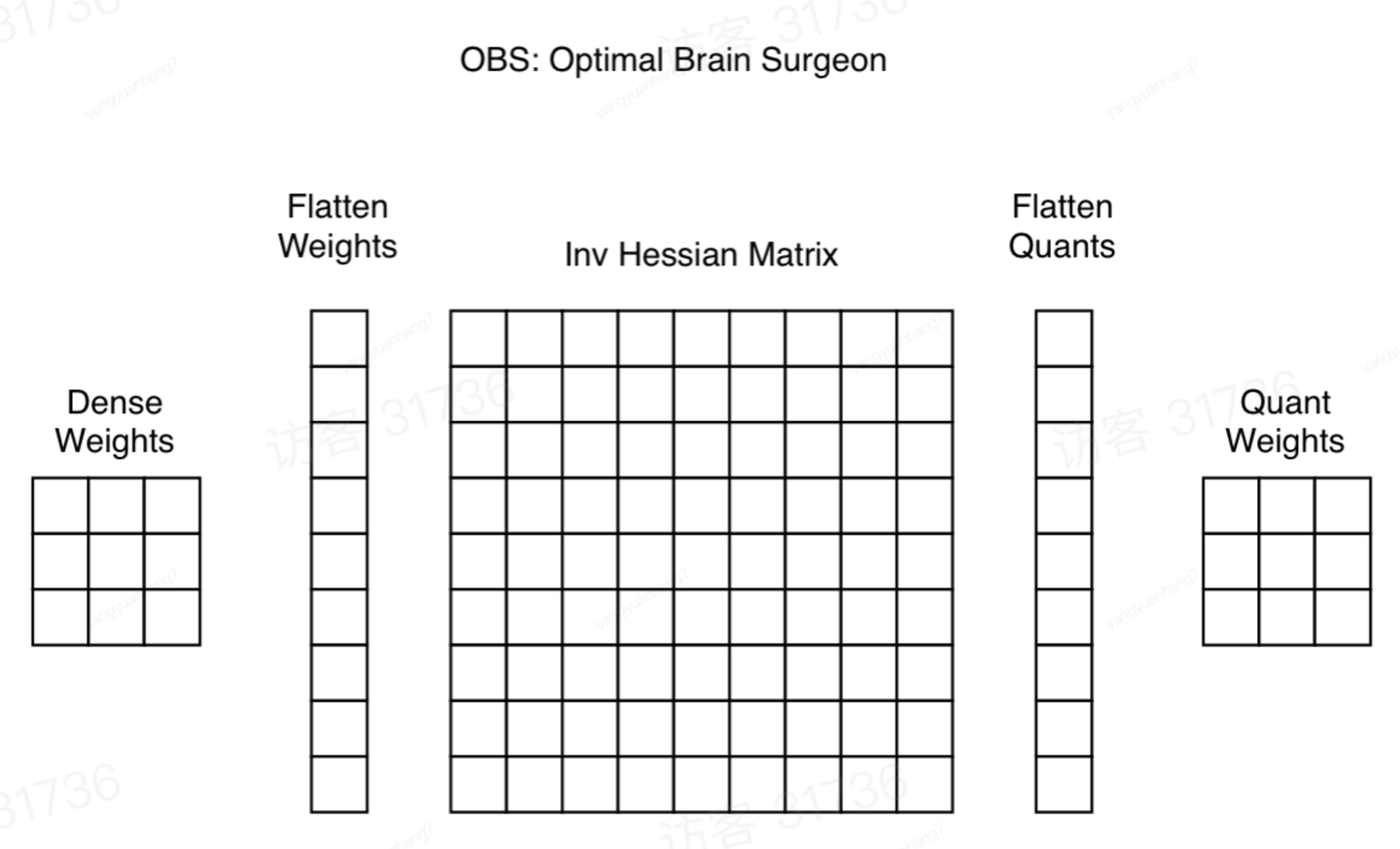
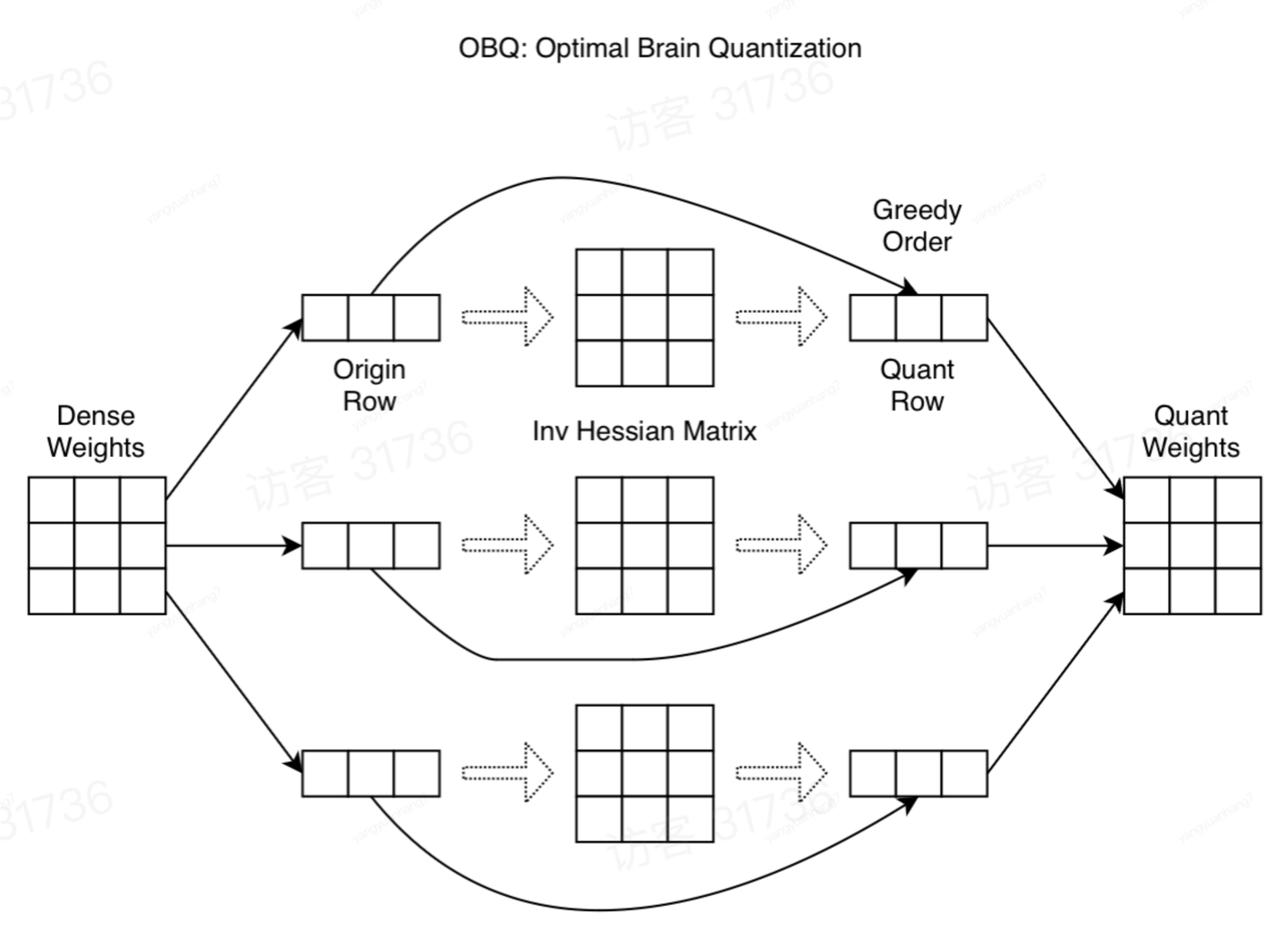
整个 OBC 的算法流程大致为:
- 对一行的权重求海森矩阵
- 按照顺序对该行的k个权重进行剪枝,并更新其他参数
- 删除海森矩阵的 p 行 p 列,再求逆
OBQ 是一种量化的方法,其将量化视为特殊的剪枝,只是把 OBC 的约束条件进行了调整:
\[\mathbf{e}_q^\text{T} \cdot \Delta \mathbf{w} + w_q = quant(w_q)\]同时把 OBC 推导公式中的 \(w_q\) 换成 \(w_q - quant(w_q)\),就得到了 OBQ 量化的参数更新公式:
\[\Delta \mathbf{w} = -\frac{w_q - quant(w_q)}{[\mathbf{H}^{-1}]_{qq}} \mathbf{H}^{-1} \cdot \mathbf{e}_q \quad \text{and} \quad L = \frac{1}{2} \frac{(w_q - quant(w_q))^2}{[\mathbf{H}^{-1}]_{qq}}\]整个 OBQ 算法的伪代码如下图所示:

- GPTQ
GPTQ 算法在前人的基础上做了一些改进。
首先是其发现当模型的参数量比较大的时候,权重量化的先后顺序带来的影响很小,所以我们干脆直接按照索引从第一个开始逐个往后量化。
其次,其假设权重矩阵的不同行权重的海森矩阵是一样的,这是因为不同行的权重处理的都是相同的输入,海森矩阵完全由未量化参数对应的输入决定。这样就可以并行地处理每一行了,大大提高了量化的速度。
为了能够缓解 IO 造成的速度瓶颈,GPTQ 将权重矩阵按列进行分组形成一个个 Block,每次量化一个 Block 的权重,其量化的规则是:当量化到某一列时,实时更新对应 Block 中的权重,而对于不在同一个 Block 且未量化的权重,先保留改变量,等一整个 Block 处理完之后再进行参数更新。
此外,GPTQ 使用 Cholesky 分解求海森矩阵的逆,在增强数值稳定性的同时,不再需要对海森矩阵做更新计算,进一步减少了计算量。(这一部分不是很懂)
整个 GPTQ 的算法流程如下:

这里海森矩阵的逆的计算值得注意,给对角线加入了一个小值 \(\lambda\) 可以减少数值计算带来的误差。(虽然不太清楚其中原理。
作者在 OPT 和 BLOOM 模型上进行了实验,结果如下图所示:
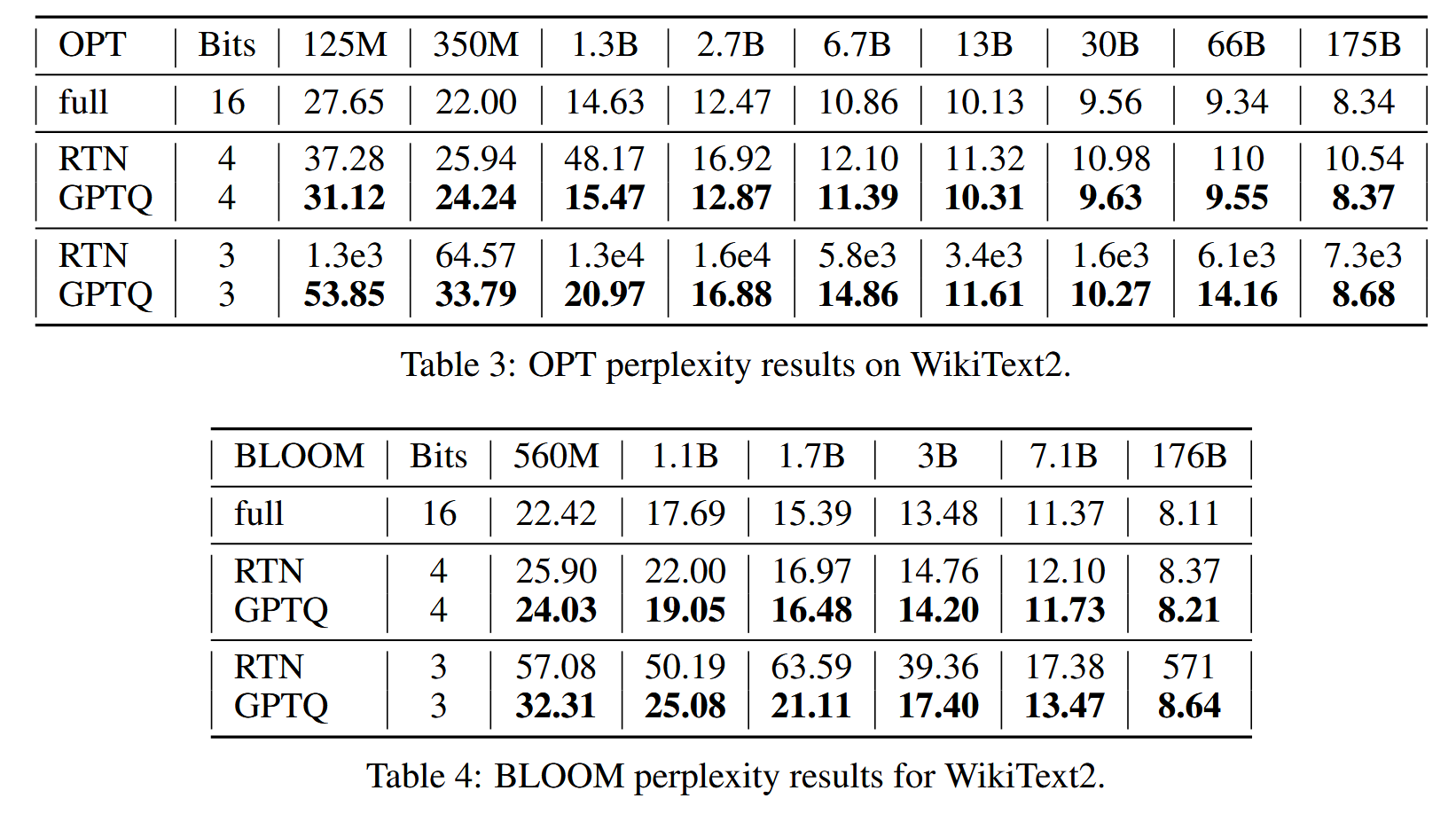
可以看到相比于 RTN 方法,GPTQ 的量化精度更高,并且更加稳定。
(3) QuIP
论文链接:https://arxiv.org/abs/2307.13304,引用次数:228,发表于:NIPS 2023
QuIP 和 GPTQ 是一样的,都使用了二次代理损失函数为目标,在优化的过程中都是一列一列地进行的。QuIP 对优化目标进行了如下转化:
\[\ell(\hat{W}) = \mathbf{E}_{x}\left[\left\|(\hat{W} - W)x\right\|^2\right] = \text{tr}\left((\hat{W} - W)H(\hat{W} - W)^T\right).\]可以变形为迹是因为存在矩阵恒等式:对于任意矩阵 A 和向量 v,我们有 \(v^TAv=tr(Avv^T)\)
同时 QuIP 采用了不同的优化方法,它并没有假设权重矩阵的所有行的海森矩阵相同,而是采用了线性层作为补偿。其原理如下:
\[\hat{W}_k = \mathcal{Q}\left(W_k + \left(W_{1:(k-1)} - \hat{W}_{1:(k-1)}\right)a_k\right)\]其中 W 的下标表示列数,a 是列向量,Q 是量化方法,可以是最近取整(nearest rounding)或标准无偏取整(standard unbiased rounding)。上式可以认为第 k 列的量化值是由前 k-1 列的量化误差决定的。如果我们把 a 写成矩阵的形式,则有:
\[\hat{W} = \mathcal{Q}\left(W + \left(W - \hat{W}\right)U\right)\]其中 U 是严格上三角矩阵。我们令
\[\eta = \mathcal{Q}\left(W + (\hat{W} - W)U\right) - \left(W + (\hat{W} - W)U\right)\]则有
\[\hat{W} - W = \eta(U+I)^{-1}\]于是我们可以把目标重写为:
\[\text{tr}\left((\hat{W}-W)H(\hat{W}-W)^T\right) = \text{tr}\left(\eta(U+I)^{-1}H(U+I)^{-T}\eta^T\right).\]我们令 \(U \leftarrow \dot{U}\) 为了能够简化上面的式子,我们可以将 H 进行分解,如下所示:
\[H = (\dot{U}+I)D(\dot{U}+I)^T\]这里的 D 是一个非负的对角矩阵,而 \(\dot{U}\) 是单位上三角矩阵(upper unit triangular)这样目标就能够化简为 \(\text{tr}(\eta D\eta^T)\),基于这样的目标再去寻找最优的 U 值会简单很多。(其可以看做是量化误差 \(\eta\) 的加权平方和)
接下来作者花了大量篇幅证明了 W 和 H 的非相干性越好,量化的效果越好,这部分的证明相当繁琐,感兴趣的同学可以自己查阅原论文,此处就简单介绍一下。
当我们谈论一个矩阵(例如,权重矩阵或Hessian矩阵)与某个基(例如,标准正交基)不相干时,意味着这个矩阵的行或列在那个基下没有表现出特别强的稀疏性或聚集性。换句话说,它的信息不是集中在少数几个方向上,而是“分散”或“均匀”分布的。
为了能够增强矩阵的不相干性,本文使用正交变换对矩阵进行处理,然后进行量化,完事了之后再反正交变换回来。
整个算法的伪代码如下图所示:


实验结果如下图所示:
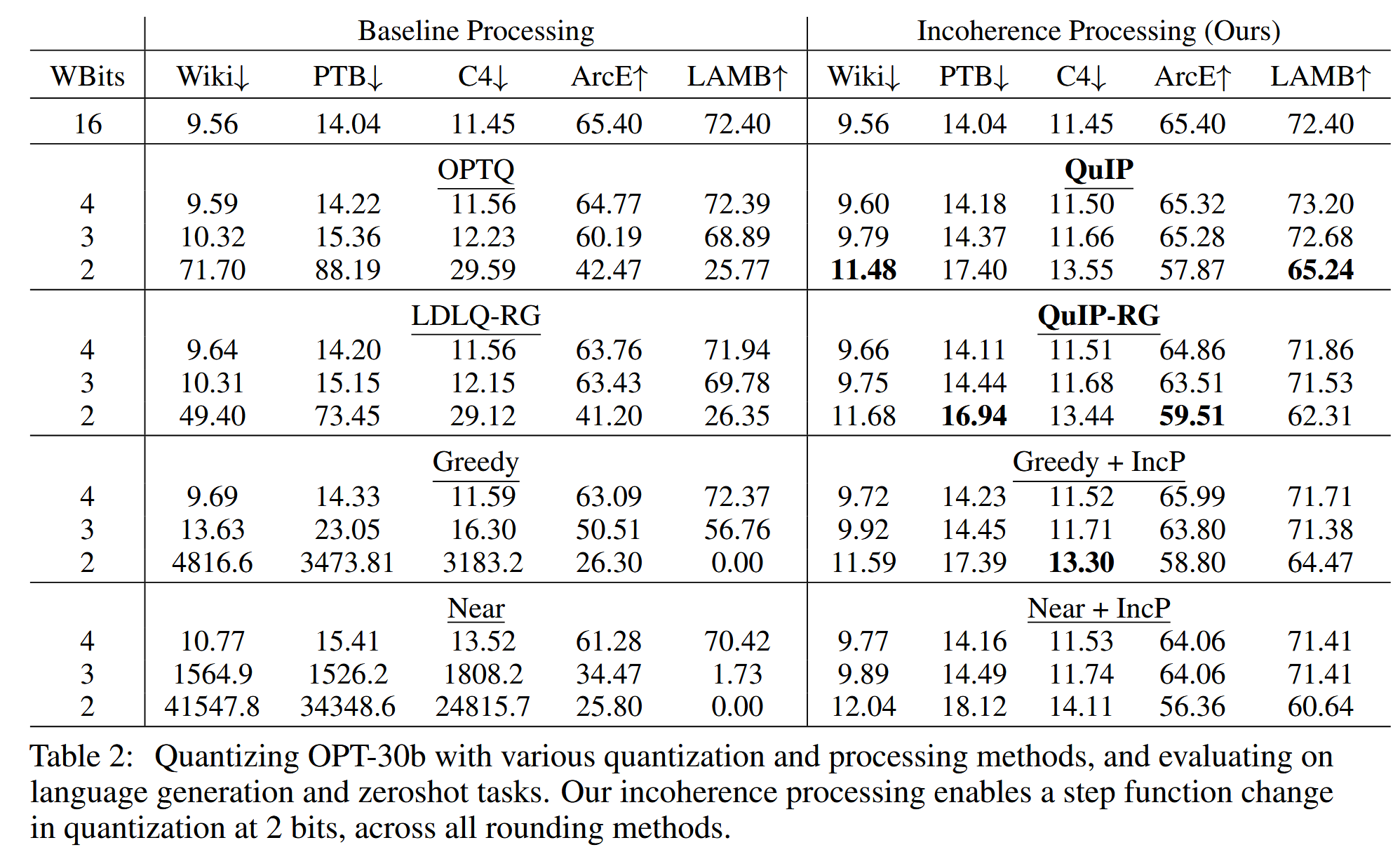
值得注意的是,这张表中右下角部分,仅仅是对原本最基础的 Greedy 和 Near 方法进行了非相干化处理,就能够大大提升其量化效果。这说明矩阵的相干性对量化的影响很大。
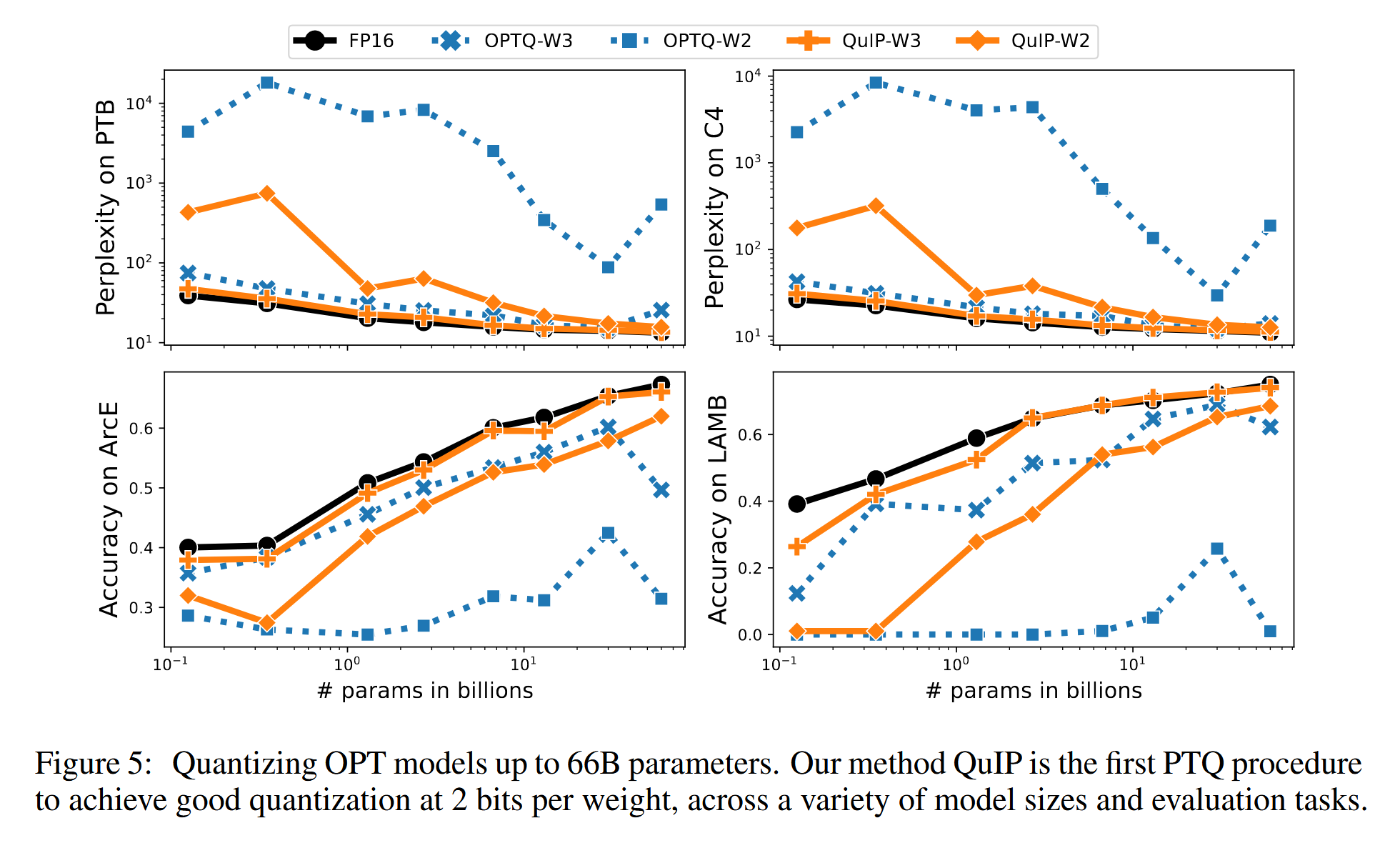
可以看到 QuIP 在 2-3 bit 低位量化上的表现令人眼前一亮,效果比 GPTQ 要好。
全篇看下来,有许多的引理、定理证明,文章比较晦涩难懂,个人以为该文的亮点就是其证明了矩阵的相干性对量化结果的影响。
(4) AWQ
论文链接:https://arxiv.org/abs/2306.00978,引用次数:1154,发表于:MLSys 2024 (best paper),作者 Ji Lin 就读于 MIT,目前在 OpenAI 工作,参与了 GPT 系列工作。其也是后面将会介绍的 Smoothquant 的共同一作。
AWQ 的全称是 Activation aware Weight Quantization,顾名思义,就是根据激活值来对权重进行量化。文章的核心思想其实很简单:神经网络中不同的权重的重要性不同,而区分其重要性的方法就是看激活值,激活值越大权重越重要(这篇文章是这么认为的,其中道理有待发掘)。在量化时,我们需要保留重要的权重来减少量化模型的精度损失。
但如果我们不对重要的权重进行量化,而是保留其 FP16 的格式,那么我们的权重是一个混合精度的数据,这在存储和处理上都存在一定的麻烦,所以我们还是需要对其进行量化的,只不过需要尽可能减少重要的权重的量化损失。
那么怎么才能在量化时保留重要的权重呢?本文提出了一种非常新奇的方法,那就是放缩。有一说一这个方法真的超级简单,其原理如下:
首先我们考虑最一般的量化方法:
\[Q(\mathbf{w}) = \Delta \cdot \text{Round}\left(\frac{\mathbf{w}}{\Delta}\right), \quad \Delta = \frac{\max(|\mathbf{w}|)}{2^{N-1}}\]这个公式应该很好理解,这里就不解释了,不理解的可以去看我之前写过的模型量化简介这一篇文章。现在我们在此基础上对权重进行放大,让其乘上一个 s,为了保持量化后的权重乘上激活值的结果不变,需要对输入除以一个 x,所以我们得到下面的公式:
\[Q(\mathbf{w} \cdot s) \cdot \frac{x}{s} = \Delta' \cdot \text{Round}\left(\frac{\mathbf{w}s}{\Delta'}\right) \cdot x \cdot \frac{1}{s}\]基于上面的两个公式,我们可以计算量化造成的误差:
\[\begin{aligned} \text{Err}(Q(\mathbf{w})x) = \Delta \cdot \text{RoundErr}\left(\frac{\mathbf{w}}{\Delta}\right) \cdot x \\ \text{Err}\left(Q(\mathbf{w} \cdot s)\left(\frac{x}{s}\right)\right) = \Delta' \cdot \text{RoundErr}\left(\frac{\mathbf{w}s}{\Delta'}\right) \cdot x \cdot \frac{1}{s} \end{aligned}\]在上面的式子中,RoundErr 其实是固定的,因为无论里面的值是多少,RoundErr 都是 [0,0.5] 的均匀分布,其期望为 0.25,所以缩放后与缩放前的误差存在比例关系:\(\frac{\Delta'}{\Delta}\cdot \frac{1}{s}\)
由于我们的量化精度取决于最大的权重,而缩放因子 s 是由激活值决定的,两者之间并不相关,所以绝大多数情况我们可以近似认为两者的量化精度是相近的,上述的比例式小于 1,因此可以利用缩放的方式减小量化损失。
所以 AWQ 的整个量化原理如下图所示:

这个方法仅仅依赖于激活值,不需要梯度信息,不需要反向传播,这意味着其实现起来超级简单,并且可以泛化到多种模态的模型上,真是相当巧妙啊,怪不得这篇文章可以获得 Best Paper,实至名归。
下面是实验相关的图表:
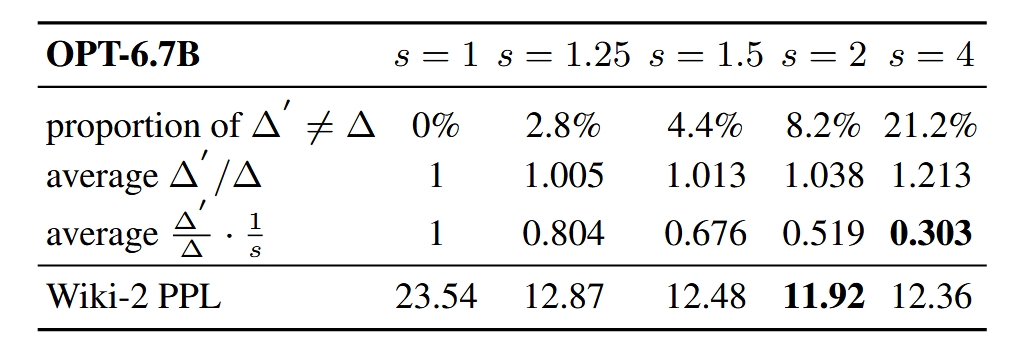
这张表说明缩放因子并不是越大越好,缩放因子大了之后,会使不显著的权重带来的影响增加。
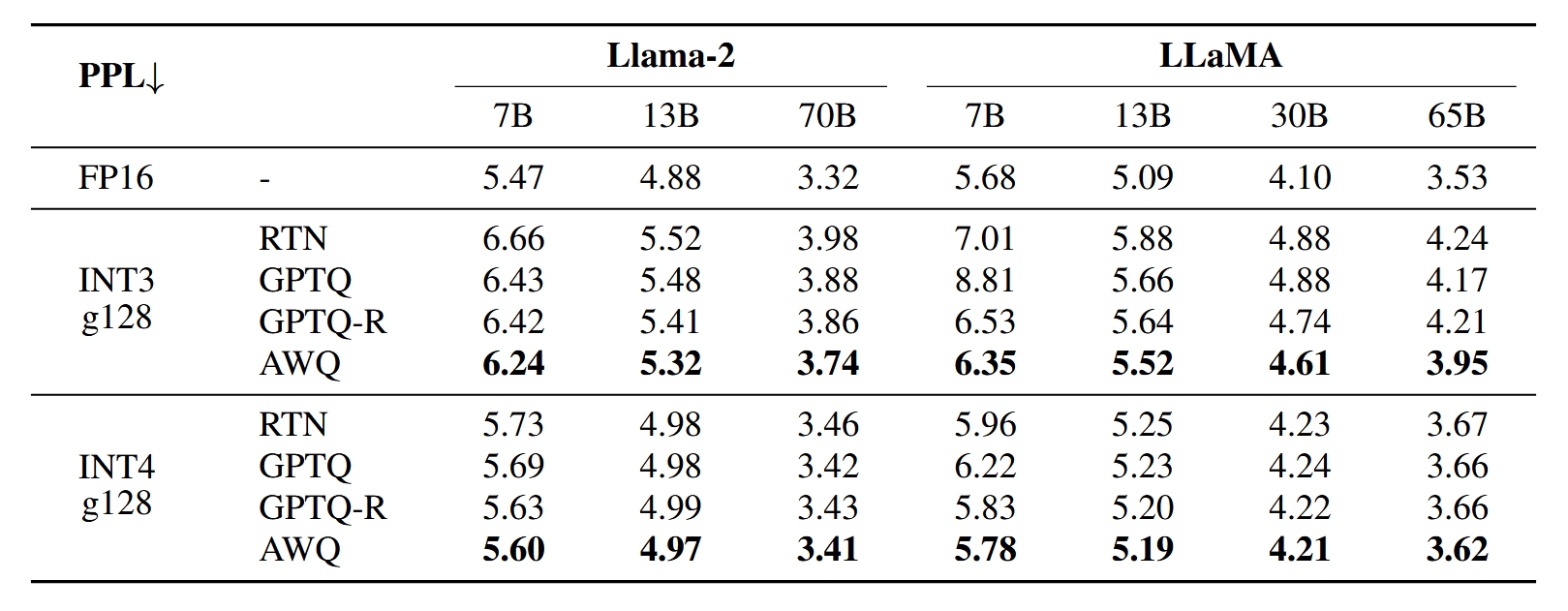
可以看到 AWQ 方法的效果还是很好的。另外文章中还有许多关于 AWQ 在多模态多任务模型上的实验结果,可以说 AWQ 简直是一个六边形战神,嘎嘎乱杀。
另外本文还有许多篇幅是介绍他们开发的一个端侧大模型部署设备 TinyChat,主要是在该设备上做了一些针对 AWQ 的优化,写了一些融合算子之类的,但这部分不是这篇文章的重点,但是可以参考其推理加速的思想。
(5) OWQ
论文链接:https://arxiv.org/abs/2306.02272,引用量:85,发表于:AAAI 2024 (oral)
OWQ 的全称是 Outlier-Aware Weight Quantization,其主要原理是根据输入和海森矩阵计算权重矩阵不同列的敏感度,将高敏感度的列进行保留,对剩下的列实行 GPTQ 量化。
量化的目标和 GPTQ 是一样的,其将量化误差写成下面的式子:
\[E_i = ||W_{i,:}X - \hat{W}_{i,:}X||_2^2 \approx \Delta W_{i,:}H\Delta W_{i,:}^T\]其中,\(\Delta W_{i,:} = W_{i,:} - \hat{W}_{i,:}\),表示第 i 行的权重矩阵变化量。这个公式是量化损失在 \(\Delta W_{i,:} = 0\) 处的泰勒展开。
有上面的式子可以看到,某一行权重带来的量化损失由该行权重的变化量和海森矩阵(其实就是输入,因为 \(H=XX^T\))共同决定。如果输入中出现了离群点,那么微小的权重变化就会带来巨大的误差。为了能够减少整体的量化损失,我们定义了敏感度(sensitivity)来衡量权重矩阵每一列的敏感度,把敏感度高的称为弱列(weak columns)。在量化的时候,保留弱列,只对其他的列进行量化操作,这样就可以大大减少量化损失。
其中敏感度的定义如下:
\[sensitivity_j = \lambda_j ||\Delta W_{:,j}||_2^2,\]其中,\(\lambda_j\) 是海森矩阵第 j 个对角元素。这是合理的,因为 H 矩阵第 i 列的和是 \(\sum_j x_ix_j = x_i \sum_j x_j\),第 i 列和第 j 列的和的比值就是 \(\frac{x_i}{x_j}\),在敏感度分析中输入造成的比例变成了上式的平方,相当于强调了输入的影响。
在量化完成需要对权重进行存储时,AWQ 采用的是一个 INT4 矩阵 + 浮点弱列向量 + 弱列索引的方式。
此外,作者还提供了一种针对 OWQ 量化后的模型进行微调的方式 WCT(Weak Column Tuning),那就是固定其他权重,仅仅调节弱列以适应不同的任务。在量化参数的设置上,采用二维网格搜索(2D Grid Search)的方式进行。(就是试参)
OWQ 方法的原理框图如下图所示:
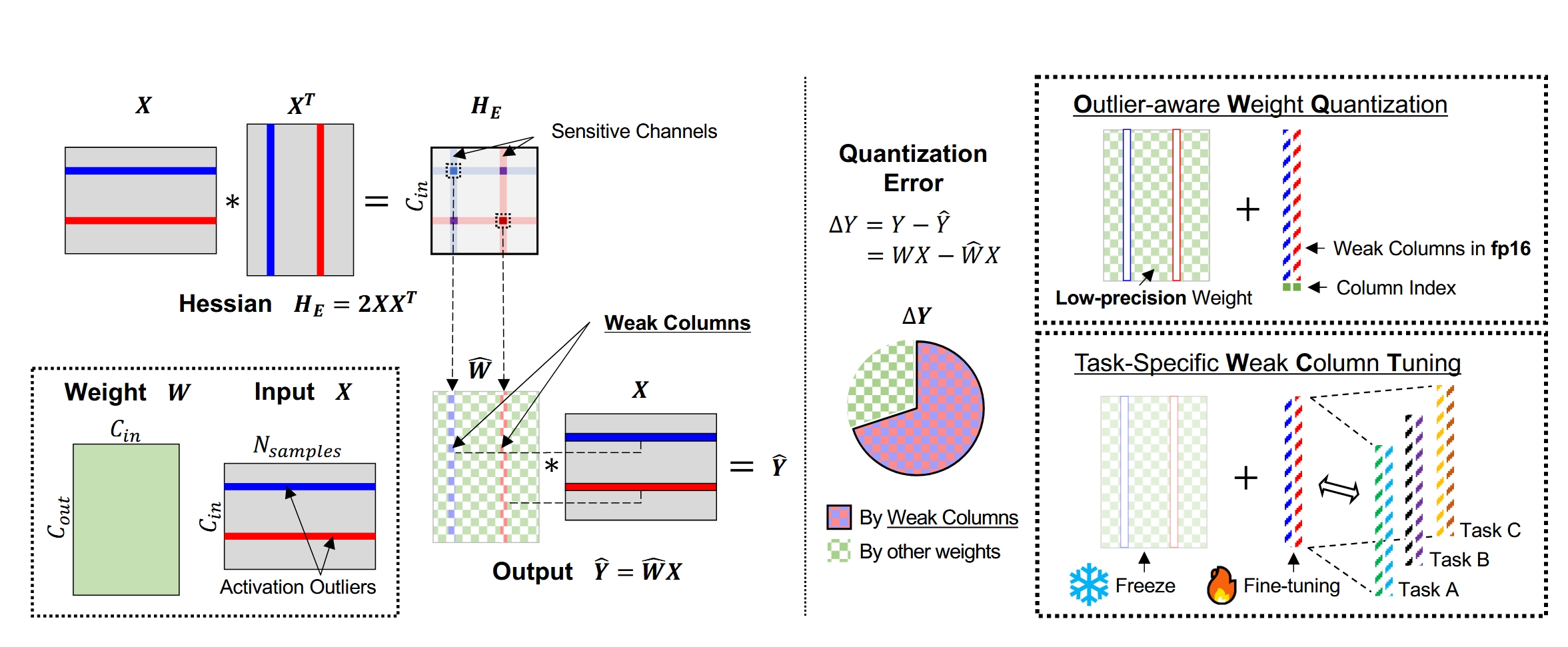
作者在 OPT 和 LLAMA 上跑了一些实验,下面是实验结果:
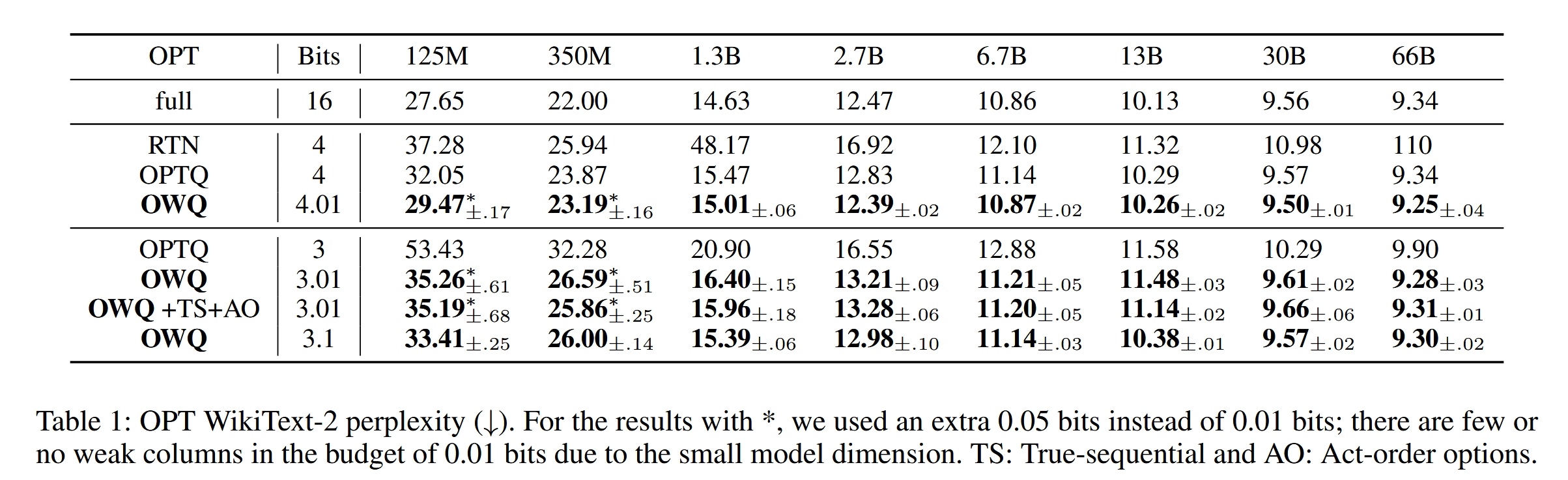
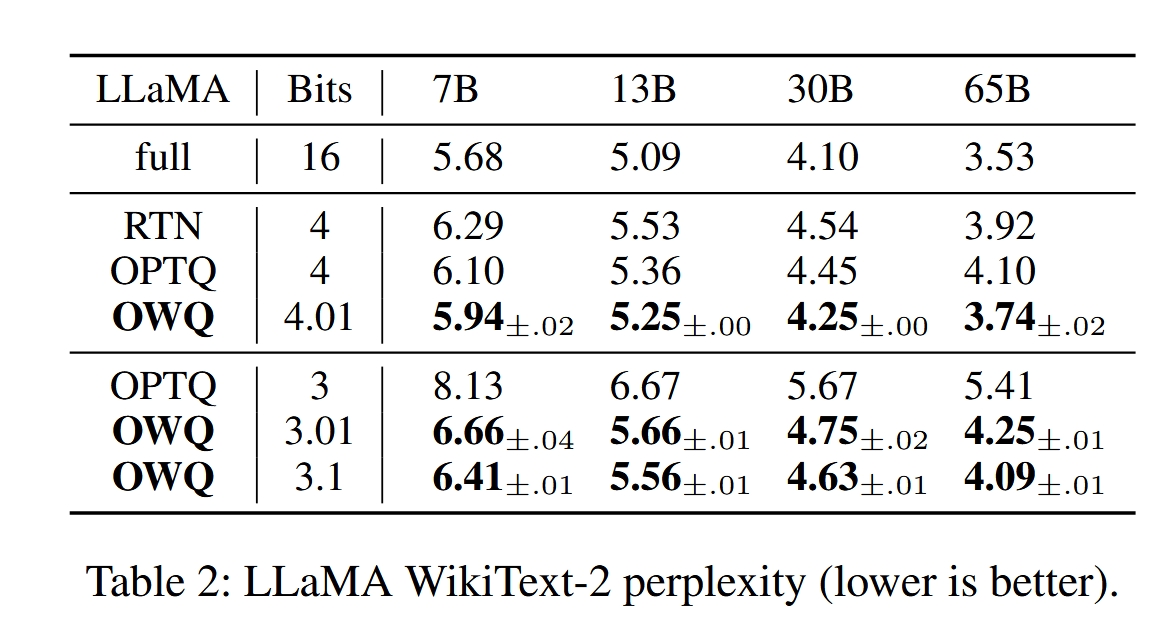
总结一下,OWQ 方法和 AWQ 其实很像,OWQ 中的 Weak columns 其实就是 AWQ 中说的 Salient weights,只不过两者对这些会带来较大量化误差权重的处理不同,前者直接保留这些权重,后者则是通过乘上一个系数来缓解其影响。这两篇文章一个是 oral,一个是 Best Paper,两篇文章发表的时间都是 23 年 6 月,撞车的结果是双方受益,令人感叹。
(6) SpQR
论文链接:https://arxiv.org/abs/2306.03078,引用量:294
Leave a comment