动量法优化详解

六月是期末月，忙着课内的事情，所以一直没有时间写博客记录，考完之后放松了几天，继续码字。

渦になる — きのこ帝国

什么是动量法

之前我们讲到神经网络优化方法，从理论的角度讲解神经网络优化存在的问题和一些可行的方法，现在我们将目光聚焦到一种特殊的优化方法上——动量法（Momentum），它的实现方法是非常简单的，公式如下：

\[\begin{aligned} z^{k+1} &= \beta z^k + \nabla f(w^k) \\ w^{k+1} &= w^k - \alpha z^{k+1} \end{aligned}\]

原理也并不难理解，就是让每一步的优化方向由该点处的梯度和前一步的方向共同决定。从直觉上看，其能够很好地解决一些病态曲率（pathological curvature）的问题，例如函数图像是一个非常窄的峡谷，正常的梯度下降可能会在两侧来回跳跃，难以收敛到最优，而使用动量法可以很好地解决这一问题。

除此之外，动量法还有着很多优势，我们需要探讨的是——为什么动量法是有效的？我们以二次凸函数为例进行分析。

二次凸函数优化

考虑这样的一个目标函数：

\[f(x) = \frac{1}{2}w^TAw - b^Tw \tag{1}\]

其中 \(w \in R^n\)，\(A\) 是对称且可逆的，所以我们可以轻松得到该函数的最小值点为 \(w^* = A^{-1}b\)，如果我们使用梯度下降的形式来表达二次凸函数优化的过程的话，我们可以得到下面的式子：

\[w^{k+1} = w^k - \alpha (Aw^k-b)\]

如果我们使用特征向量作为基底来表示向量，那么就可以对 \(w\) 的每一个维度分别处理。首先我们将 A 变换为对角矩阵：

\[A = Q\Lambda Q^T\]

其中 \(\Lambda\) 是由特征值 \(\lambda_1, \lambda_2, \dots, \lambda_n\) 按照从小到大的顺序排列的对角矩阵。然后我们令 \(x^k = Q(w^k-w^*)\)，于是 (1) 式可以重写为下面的形式：

\[\begin{align*} x_i^{k+1} &= x_i^k - \alpha\lambda_ix_i^k \\ &= (1-\alpha\lambda_i)x_i^k \\ &= (1-\alpha\lambda_i)^{k+1}x_i^0 \end{align*}\]

从这个式子中，我们可以发现当 \(0 < \alpha\lambda_i < 2\) 时，我们的参数会逐渐收敛到最优解处，并且收敛的速度是由最大和最小的特征值决定的：

\[rate(\alpha) = \max \{|1-\alpha\lambda_1|, |1-\alpha\lambda_n|\}\]

当最大和最小的两个特征值对应的收敛速度一样时，整体的收敛速度是最快的，所以我们可以取步长：

\[\alpha = \frac{2}{\lambda_1 + \lambda_n}\]

此时我们有收敛速率：

\[rate(\alpha) = 1-\alpha\lambda_n = \frac{\lambda_n - \lambda_1}{\lambda_n + \lambda_1} = \frac{\lambda_n / \lambda_1 - 1}{\lambda_n / \lambda_1 + 1}\]

有上式可以看到，实际的收敛速率是由最大特征值与最小特征值的比值决定的，我们称 \(\kappa = \frac{\lambda_n}{\lambda_1}\) 为条件数（condition number）。

接下来让我们重新聚焦于动量算法，其公式被我们重写为下面的形式：

\[\begin{aligned} z^{k+1} &= \beta z^k + (Aw^k-b) \\ w^{k+1} &= w^k - \alpha z^{k+1} \end{aligned}\]

通过与上面类似的操作，我们在把特征向量作为基的空间中考察上式的特性：

\[\begin{aligned} y_i^{k+1} &= \beta y_i^k + \lambda_ix_i^k \\ x_i^{k+1} &= x_i^k - \alpha y_i^{k+1} \end{aligned}\]

可以看到动量法中，方向和速度的每一个分量都可以认为是相互独立的，如果我们使用矩阵的形式重写，就能够得到下式：

\[\left(\begin{array}{c} y_i^k \\ x_i^k \end{array}\right) = R^k \left(\begin{array}{c} y_i^0 \\ x_i^0 \end{array}\right) \quad R = \left(\begin{array}{cc} \beta & \lambda_i \\ -\alpha\beta & 1 - \alpha\lambda_i \end{array}\right).\]

二阶矩阵的 k 次方的求解有许多种方法，一种比较常见的方法是利用特征多项式求解，过程就不多说了，感兴趣的同学可以自行搜索，最后得到的结论如下：

\[R^k = \begin{cases} \sigma_1^k R_1 - \sigma_2^k R_2 & \sigma_1 \neq \sigma_2 \\ \sigma_1^k (kR/\sigma_1 - (k-1)I) & \sigma_1 = \sigma_2 \end{cases}, \quad R_j = \frac{R - \sigma_j I}{\sigma_1 - \sigma_2}\]

为了能够让其收敛，我们需要让 R 的特征值绝对值小于 1，在此条件下，我们可以推导出下面的收敛条件：

\[0 < \alpha\lambda_i < 2+2\beta \quad for \quad 0 \leq \beta <1\]

可以看到，相比较于梯度下降，\(\alpha\) 的取值范围扩大了，这意味着在更大的范围内调整超参数，都能够保证收敛的结果。这就是动量算法的优势。

动量法的最优参数和收敛率

为了能够取得整体最优的收敛速度，我们需要同时对 \(\alpha,\beta\) 进行优化，求解的过程是非常繁琐的，但最后得到的结果如下：

\[\alpha = \left( \frac{2}{\sqrt{\lambda_1} + \sqrt{\lambda_n}} \right)^2 \quad \beta = \left( \frac{\sqrt{\lambda_n} - \sqrt{\lambda_1}}{\sqrt{\lambda_n} + \sqrt{\lambda_1}} \right)^2\]

把上面的结果代入收敛速率中，我们得到：

\[\frac{\sqrt{\kappa} - 1}{\sqrt{\kappa} + 1} \quad \text{Convergence rate}\]

相比较于直接梯度下降的收敛率：

\[\frac{\kappa - 1}{\kappa + 1}\]

其提升是非常明显的，如果条件数 \(\kappa = 100\)，则梯度下降的收敛率为 0.98，而动量法的收敛率为 0.818，在经过多轮迭代之后，两者速度相差更加悬殊。

但动量法同样是存在局限的，动量法在处理单一路径构成的染色问题中具有局限性，因为每一步迭代只能对一个结点进行染色，所以至少需要 n 轮迭代，这和其他的基于一阶最优条件的算法（first order algorithm）是一样的。

基于随机梯度的动量法

由于我们所采用的是小样本的梯度，其本身是带有随机性的，我们可以认为其是在真实梯度的基础上添加了一个误差项得到的。

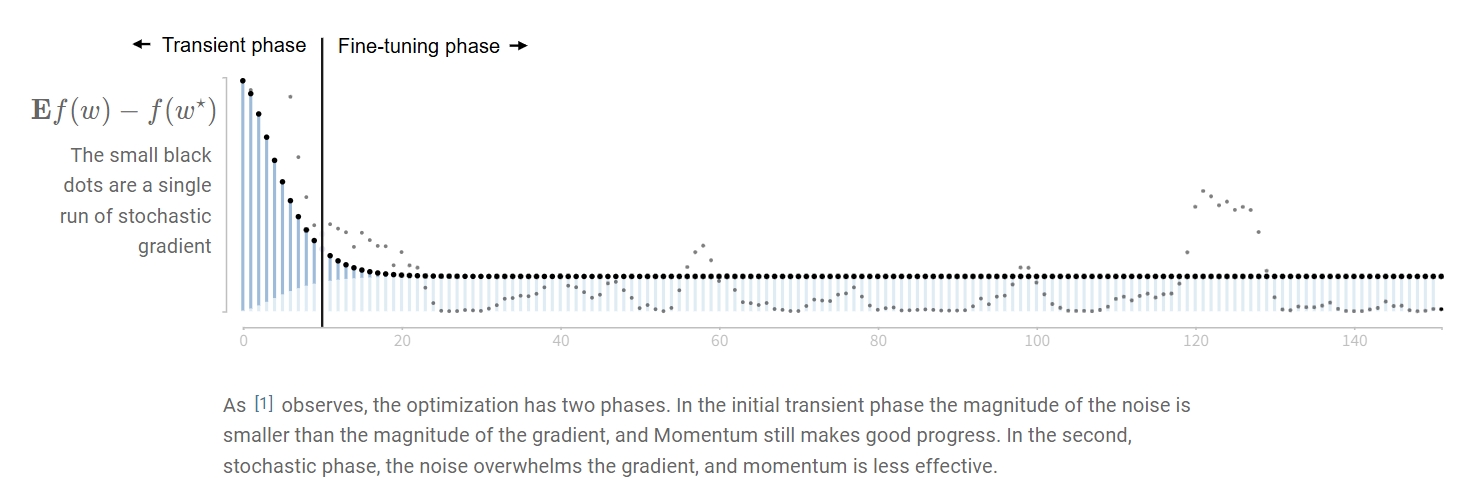
于是动量法优化的过程就可以分成两个阶段，如下图 1 所示：

图 1 动量法优化时的目标函数误差变化

• 瞬态阶段 (Transient Phase)：在这个初始阶段，噪声的幅度小于梯度的幅度，动量仍然能取得显著进展。目标函数值快速下降。

• 微调阶段 (Fine-tuning Phase)：随着接近最小值，噪声开始压倒梯度信号，动量的效果变差。目标函数值停止显著下降，可能在最优值附近波动。

于是就存在误差成分之间的权衡：减小步长可以减少随机误差，但会减慢收敛速度；增加动量可能导致误差累积（这与直觉不同）。

尽管有这些“不良”特性，但带有动量的随机梯度下降在神经网络中表现出色。最近的研究甚至认为，这种噪声是件好事——它起到了一种隐式正则化的作用，类似于早停，有助于防止在优化的微调阶段出现过拟合。

总结

总而言之，动量法是一个非常有效的优化方法，它比梯度下降收敛更快，同时超参数的可调整范围也更大。比较值得注意的就是动量法的参数范围和收敛率。我也没想到简单的公式背后居然有这么复杂的数学原理，不得不感叹做理论那帮人真的厉害。

参考文献：

Why Momentum Really Works