关于梯度消失和梯度爆炸

梯度消失和梯度爆炸在初期一直是深度神经网络训练的一个难点，但前人做的许多工作已经基本上解决了这个问题。但研究这个问题还是有必要的，其涉及到神经网络优化的基本原理。

Funeral — Arcade Fire

缓解梯度消失和梯度爆炸的方法

• 残差连接

任何搞深度学习的人都知道何凯明大神的著作 [1512.03385] Deep Residual Learning for Image Recognition，其提出了残差连接的方式，解决了梯度消失的问题，让更深的神经网络更容易训练，且其效果不逊色于浅层神经网络。

关于残差连接是如何解决梯度消失问题的，详细的公式推导或许还不如直觉上的理解，其实就可以简单地认为残差连接将梯度进行了分流，分成了两个部分的和，其中有一个恒等映射的梯度是 1，所以梯度可以通过这一部分传到后续的层中。

图 1：残差连接示意图

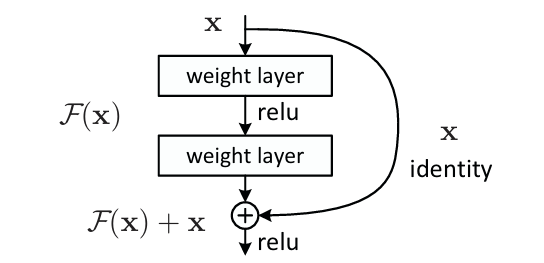
另外，残差网络的另一个思想就是，深层网络应该具有不逊色于浅层网络的效果，毕竟只要多出来的层是一个恒等映射就能保证效果持平。然而让神经网络学习一个恒等映射比全零映射要困难得多，所以我们干脆人为地把输入加到输出中去，这样网络的部分只要学习全零映射，整个模块就能够实现恒等映射的效果。

此外还有许多方法来解决梯度消失和梯度爆炸的问题：

• 激活函数

原来的神经网络使用 tanh 或者 sigmoid 函数来作为激活函数，但是这些函数在权重绝对值大的地方梯度近似为 0，多层网络的叠加会导致梯度非常接近于 0，造成梯度消失。Relu 激活函数的提出解决了这一问题，它在任何大于 0 的点处梯度都是 1，梯度在进行传递时不会有缩放效应。

• 权重正则化与初始化

权重正则化是避免梯度爆炸的一个方法，其在损失项中加入模型的权重，防止模型的权重过大导致梯度累乘的结果过大。另外初始化也是有讲究的，一般会将模型的参数初始化为均值为 0 的正态分布。

• 批归一化

初始化与权重正则化是针对神经网络参数的优化，BN（Batch Normalization）操作则是针对网络输入进行的优化，它保证了输入遵循特定的分布，不会发生偏移，使模型更好训练，也缓解了梯度的问题。

GRU 网络与梯度消失

GRU（gated recurrent units）是对循环神经网络 RNN 的一个改进，其在 LSTM 之后提出，使用了更新门（update gate） 和 重置门（reset gate） 来捕获序列中长期和短期的依赖关系，控制信息的遗忘与传递，从而缓解梯度消失/爆炸问题。

其基本原理如下所示：

• 输入序列：\(x_t \in \mathbb{R}^n\)
• 上一时刻的隐藏状态：\(h_{t-1} \in \mathbb{R}^d\)
• 当前时刻输出：\(h_t \in \mathbb{R}^d\)

更新门（update gate）：控制当前状态有多少来自过去（记忆） vs 当前输入（新信息）

\[z_t = \sigma(W_z x_t + U_z h_{t-1} + b_z)\]

重置门（reset gate）：控制前一状态对当前候选状态的影响程度

\[r_t = \sigma(W_r x_t + U_r h_{t-1} + b_r)\]

其中：

• $\sigma$ 是 sigmoid 函数，输出在 $(0, 1)$
• $W_z, U_z, W_r, U_r$ 是待学习的权重矩阵

计算候选隐藏状态（新记忆）：

\[\tilde{h}_t = \tanh(W_h x_t + U_h (r_t \odot h_{t-1}) + b_h)\]

• 这里使用重置门 $r_t \odot h_{t-1}$ 来控制前一状态的贡献；
• 如果 $r_t \approx 0$，表示“忘掉之前的信息”；
• 如果 $r_t \approx 1$，表示“完全保留之前的信息”。

计算最终隐藏状态（平衡新旧信息）：

\[h_t = (1 - z_t) \odot h_{t-1} + z_t \odot \tilde{h}_t\]

关于 GRU 网络为什么能缓解梯度消失的问题，可以看其计算最终隐藏状态的公式，它把梯度分成了两部分的和，允许梯度直接从上一层流动过来，采用的是和 ResNet 一样的梯度分流的策略。极端情况下如果 \(z_t = 0\)，结果就相当于直接把上一个状态复制过来。

所以其实我们可以看出，GRU 和 ResNet 的思想还是很相似的，GRU 是 2014 年提出的，ResNet 是 2015 年提出的，两者就相差了一年时间，或许何凯明参考了 GRU 的这部分思想也说不准？:)